porttraveler.blogg.se - Recursive formula for arithmetic sequence definition

Recursive formula for arithmetic sequence definition how to#
Recursive formula for arithmetic sequence definition trial#
Recursive formula for arithmetic sequence definition series#

The explicit formula is used to find the term of a sequence irrespective of information about its previous term.\) So each term must be larger than the last. The recursive formula is used to find a term of a sequence when its previous term is known.

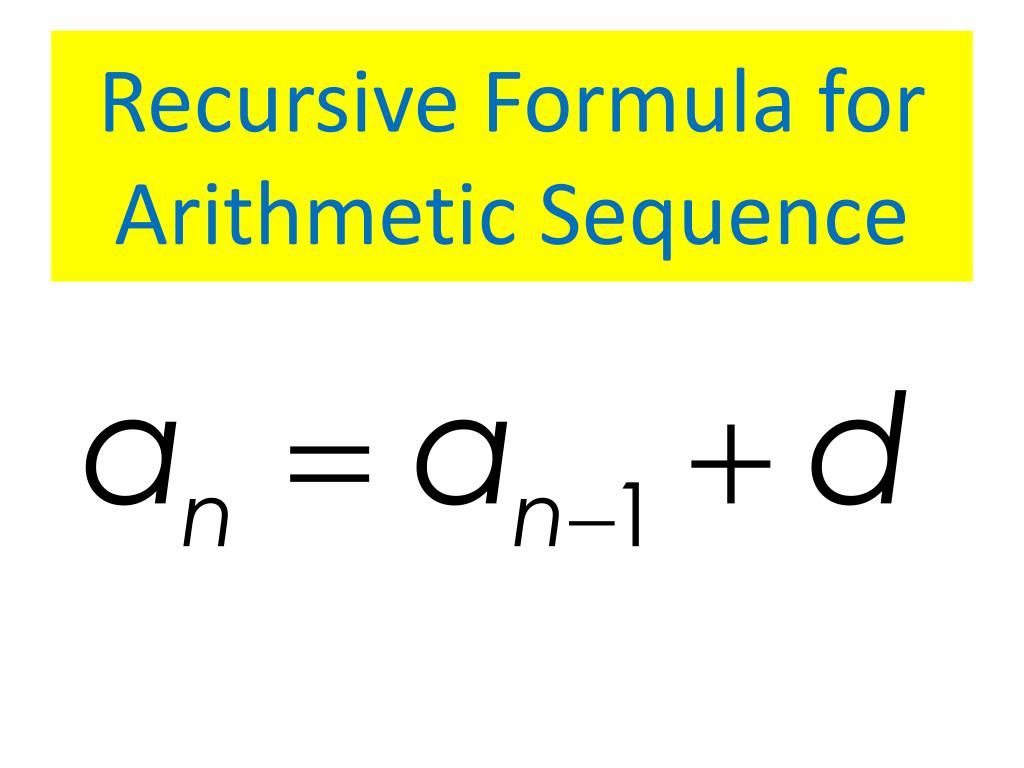
An explicit formula for an arithmetic sequence with common difference d. As with any recursive formula, the initial term of the sequence must be given. What is the Difference Between Recursive and Explicit Formulas? A recursive formula for an arithmetic sequence with common difference d.

n th term of a Fibonacci Sequence: a n = a n-1 + a n-2 for n ≥ 2.

n th term of G.P: a n = a n-1 for n ≥ 2.

n th term of A.P: a n = a n-1 + d for n ≥ 2.

In any recursive formula, a n refers to the n th term in the sequence, which can be found using the recursive formulas:

Thus, the Fibonacci formula is given as, F n = F(n-1) + F(n-2), where n > 1.

Recursive formula for arithmetic sequence definition series#

The Fibonacci series is characterized as the series in which each number is the sum of two numbers preceding it in the sequence. What is the Recursive Rule For the Fibonacci series?

Step 2: Put the values in the formula, a n+1 = a n + d to find the (n+1) th term to find the successive terms.

Step 1: Identify the n th term (a n) of an arithmetic sequence and the common difference, d,.

In order to define an arithmetic sequence, we need to be given or determine the common difference and the first term. f o r In other words, a term in an arithmetic sequence is found by adding the common difference to the previous term. To find a recursive sequence in which terms are defined using one or more previous terms which are given. As we may note from the definition, the recursive formula for the arithmetic sequence can be written as +, 1.

Recursive formula for arithmetic sequence definition how to#

How to Find the Recursive Formula for an Arithmetic Sequence? Here, a n represents the n th term and a n-1 represents the (n-1) th term.

The recursive formula of a geometric sequence is, a n = a n-1r.

The recursive formula of an arithmetic sequence is, a n = a n-1 + d.

Using the recursive formula for the Fibonacci sequence,ġ5 th term is the sum of 13 th term and 14 th term.Īnswer: The 15 th term of the Fibonacci sequence is 377.įAQs on Recursive Formula What is the Recursive Formula in Math?Ī recursive formula is a formula that defines any term of a sequence in terms of its preceding term(s).

Let a n be the n th term of the series and d be the common difference.Īnswer: The recursive formula for this sequence is a n = a n-1 + 5Įxample 3: The 13 th and 14 th terms of the Fibonacci sequence are 144 and 233 respectively. Given that f(0) = 0.Įxample 2: Find the recursive formula for the following arithmetic sequence: 1, 6, 11, 16.

Recursive formula for arithmetic sequence definition trial#

With Cuemath, find solutions in simple and easy steps.īook a Free Trial Class Examples Using Recursive RuleĮxample 1: The recursive formula of a function is, f(x) = 5 f(x-2) + 3, find the value of f(8). Use our free online calculator to solve challenging questions. Let us see the applications of the recursive formulas in the following section. A recursive function is a function that defines each term of a sequence using the previous term i.e., The next term is dependent on the one or more known previous terms. Where a n is the n th term of the sequence. The recursion step consists of a set of rules that reduces the successive cases to forward to the base case. The recursive formula to find the n th term of a Fibonacci sequence is: The recursive formula to find the n th term of a geometric sequence is: The recursive formula to find the n th term of an arithmetic sequence is: Recursive Formula for Arithmetic Sequence The following are the recursive formulas for different kinds of sequences.

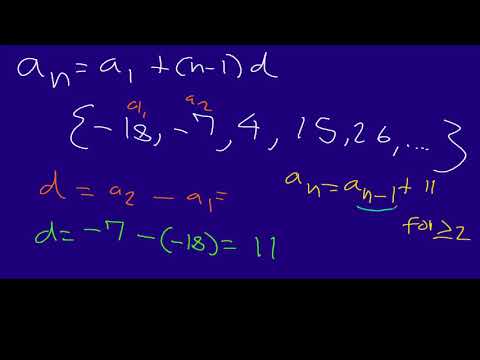
The pattern rule to get any term from its previous term.The recursive formulas define the following parameters: What Are Recursive Formulas?Ī recursive formula refers to a formula that defines each term of a sequence using the preceding term(s). Let us learn the recursive formulas in the following section. + a x-1 h(x-1) where a i ≥ 0 and at least one of the a i > 0 A recursive function h(x) can be written as: where the next term is dependent on one or more known previous term(s). A recursive function is a function that defines each term of a sequence using a previous term that is known, i.e. Before going to learn the recursive formula, let us recall what is a recursive function.